Path Tracing
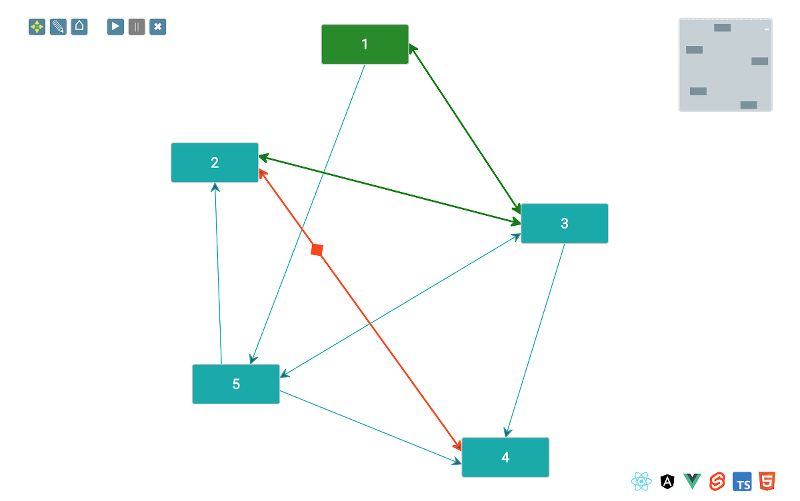
< Back to demo listThis is a demonstration of the path tracing functionality. Nodes here are positioned randomly and then moved as if they were connected with springs to each other, using the ForceDirected layout.
Click a node to select it. Then click another node. The shortest path between the two nodes will be traversed with an overlay. If no path exists (which can happen due to the fact that edges may be one-way), an alert will show.
Use the pause/play/cancel buttons to change the state of the path trace animation.

The source code for this application - and several others - is available on Github here. If you haven't got a license for the Toolkit, we offer 30 day evaluations.
A graph is a structure that consists of a set of objects in which some set of pairs are related. The objects in the set are variously referred to as vertices or nodes, and sometimes points. The relationship between any two vertices is referred to as an edge, or link. Edges may be directed or undirected.Wikipedia gives a good example of directed vs undirected edges:
For example, if the vertices represent people at a party, and there is an edge between two people if they shake hands, then this graph is undirected because any person A can shake hands with a person B only if B also shakes hands with A. In contrast, if an edge from a person A to a person B means that A owes money to B, then this graph is directed, because owing money is not necessarily reciprocated
Edges may also be weighted, which is the concept of how "expensive" it is to travel along that edge. A good analogy for this can be found in road networks: when a particular road is choked with traffic, we'd assign it a high weight value, whereas roads that have little to no traffic would be assigned a low value. Of course this is a simplified take: the weight of a road segment is more properly a measure of its current throughput, and in the real world we'd take into account how many lanes has, what the average speed is, etc. Interestingly, the nucleus of the Toolkit's data model came directly from some JS code we wrote many years ago as part of a road traffic simulation.
A Path is a sequence of vertices in which the target vertex of one edge is the source vertex of the next edge in the path. Where a graph contains directed edges, it may be the case that some vertex is not reachable from some other vertex, ie. there is no path available.
There are a number of different algorithms that are used to calculate paths in graphs. One of the most well-known, and the one that the Toolkit uses, isDjikstra's algorithm. In summary, Djikstra's algorithm works by assigning a 'distance' value for every vertex in the graph except for the source vertex, with an initial value of Infinity for each vertex. From the source vertex we find its neighbours, and then compute the distance to that neighbour from the weight of the edge. We then repeat the process using each of the neighbours as the focus. Each time we process a neighbour we check to see if our new computed distance to that neighbour is less than a previously computed distance, and if so, we store it. Once all the distance to every vertex has been computed we track back from the target vertex along the path represented by the minimum distance.
The Toolkit has at its core an implementation of a graph. Whenever you add a node to an instance of the Toolkit, that node is added as a vertex to the underlying graph. Whenever you establish a connection between two nodes, that connection is added as an edge to the underlying graph. This foundation adds a great deal of power to the Toolkit - you can reason with and interrogate its data model.
As mentioned above, the Toolkit uses the Djikstra algorithm to computer paths between vertices, but in fact we use a modified version which is able to take "ports" into account.
The Toolkit offers a number of methods for working with paths, which are discussed on our site here: https://docs.jsplumbtoolkit.com/toolkit/6.x/lib/paths.
The Toolkit's Surface renderer offers a complete solution for tracing paths through the UI. As shown in the demo above, there is a transport control available, and throughout the lifecycle of a path trace a number of CSS classes are used. You can read about path tracing in full on our site here: https://docs.jsplumbtoolkit.com/toolkit/6.x/lib/path-tracing.
Flowchart Builder
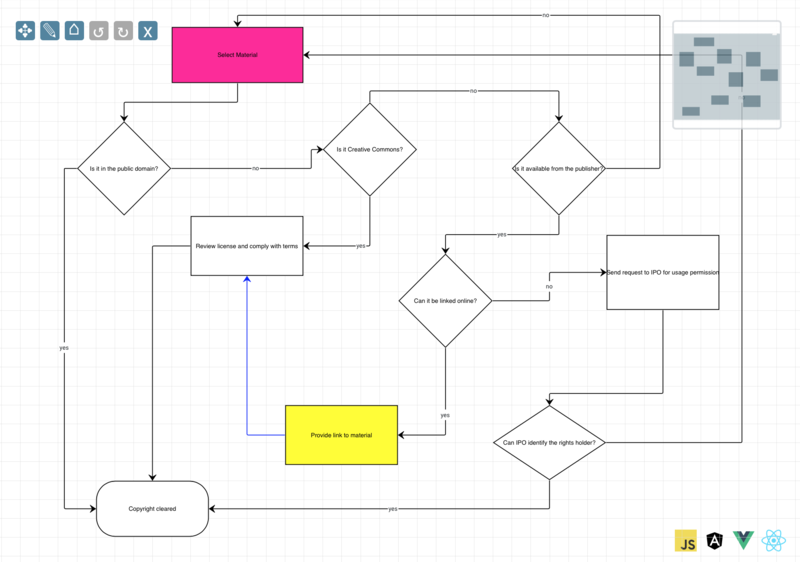
Schema Builder
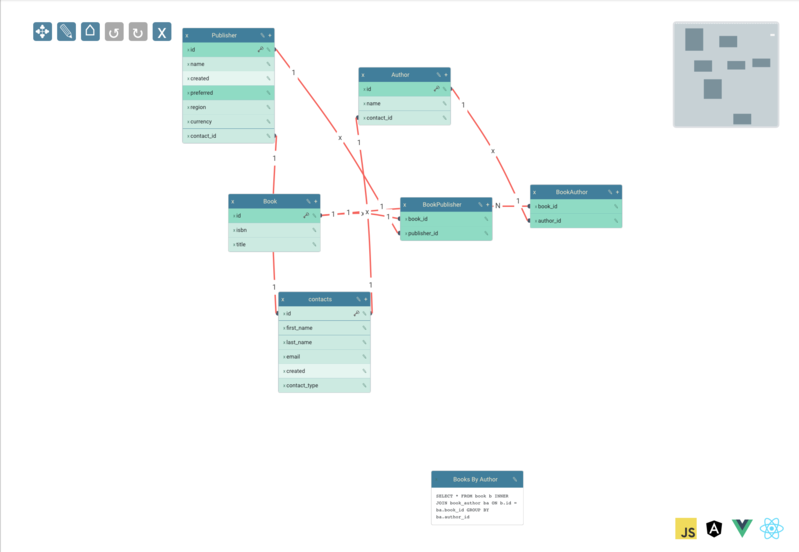
Chatbot Builder
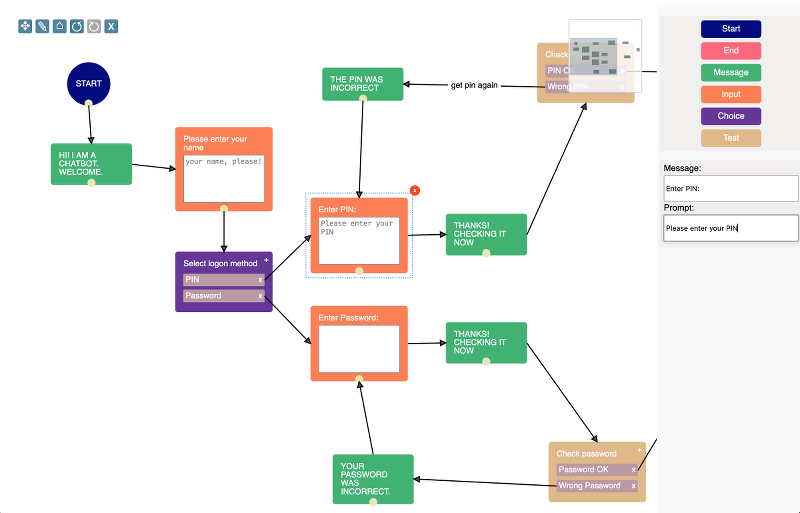
Org chart
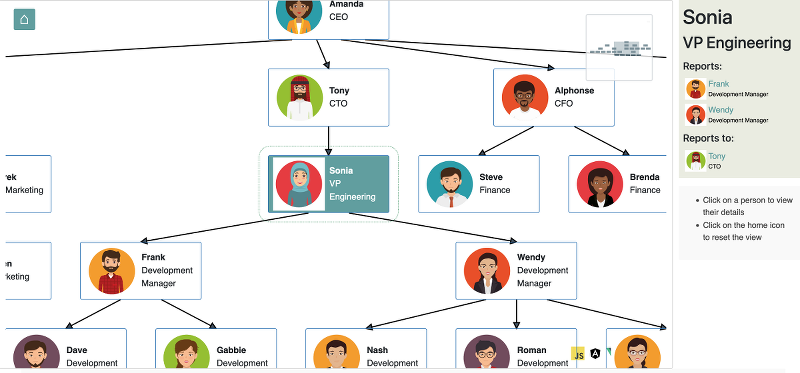
Mindmap Builder
Nested Groups
Hello World
Image Processor
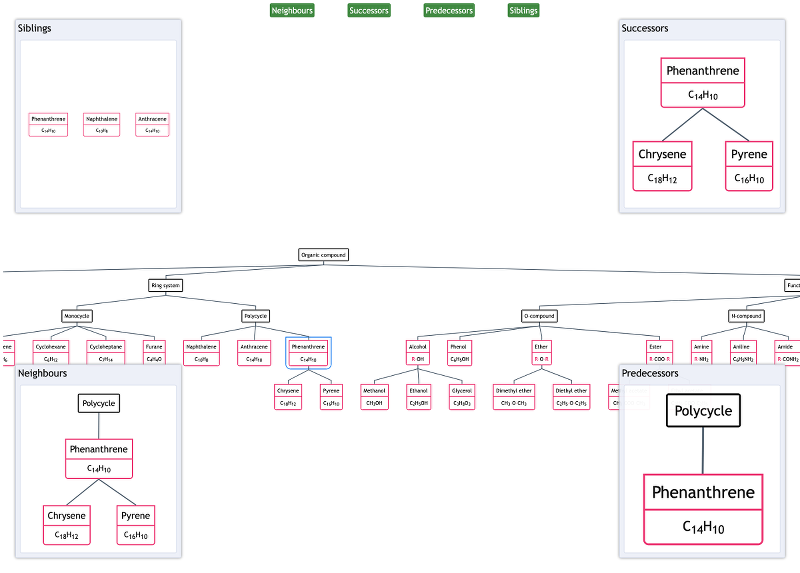
Neighbourhood Views
Active Filtering
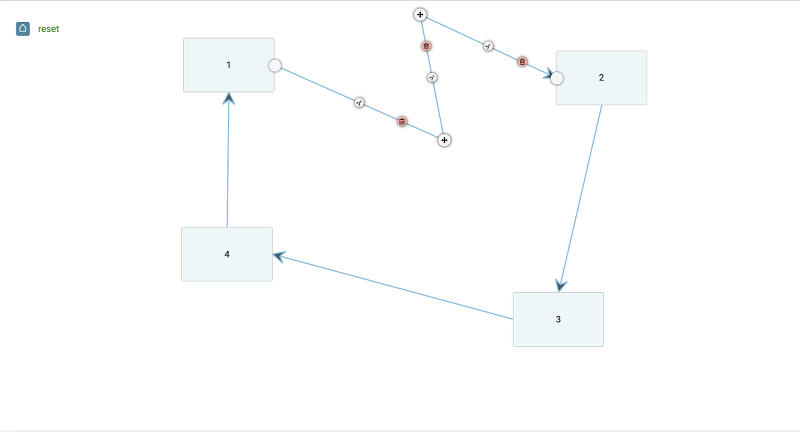
Segmented Connectors
Hierarchy Layout
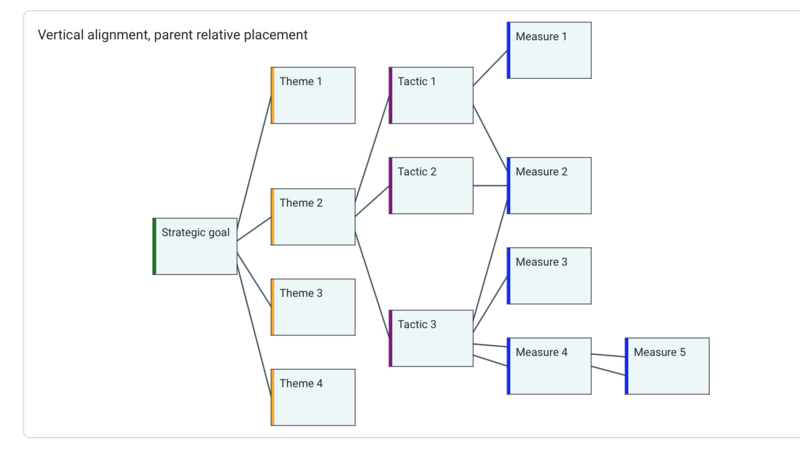
Layouts